The Lawn Mowing Problem

Summary

(Fekete et al. 2023)

Continuous generalization of the traveling salesman problem (TSP).

Tour starts and ends at the same point, covers every point.

Prerequisites

• Galois groups
• Abelian property
• Polyminoes
• Minkowski sums

Galois groups

Polynomials are solvable by radicals iff they have enough symmetry.

i.e. iff their Galois group is abelian (commutative)

Polynomials of order < 5 are algebraically easy

• Can be solved by radicals

\( \frac{-b \pm \sqrt{b^2-4ac}}{2a} \)

Most polynomials of order ≥ 5 are algebraically hard

• Cannot be solved by radicals

Polyminoes

Generalized dominoes.

Shapes made up of pixels.

Minkowski sums

\( {\color{red} R} = {\color{green} G} \bigoplus {\color{blue} B} = \{ \mathbf g + \mathbf b\ |\ \mathbf g \in {\color{green} G},\ \mathbf b \in {\color{blue} B} \} \)

Real world

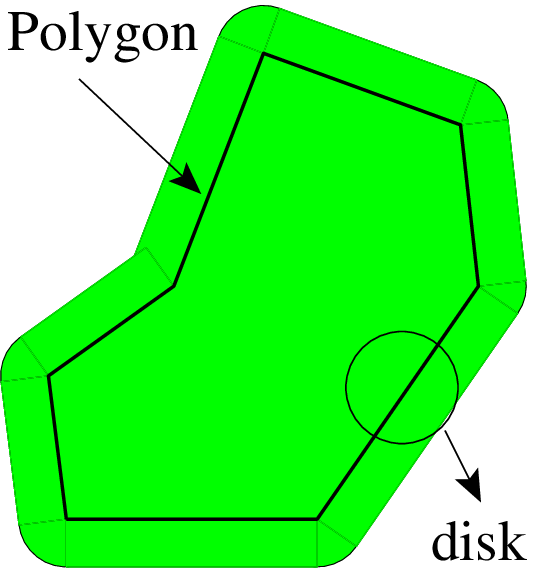
Efficient covering of polyminoes

Efficient covering of pixels

Traveling Salesperson

Problem is now reduced to the traveling salesperson problem. Solution:

• Integer Programming (IP)
• Large Neighborhood Search (LNS)

Lower & Upper Bounds

Conclusion

Already proven:

• the optimal tour of a polygon is polygonal itself

Proven in this paper

• the coordinates are algebraically hard

Future research:

• Better lower bounds

References